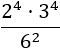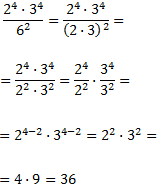En esta página vamos a ver las propiedades de las potencias, que son muy importantes porque nos permiten simplificar mucho las expresiones algebraicas.
En la mayoría de las propiedades, las bases de las potencias tienen que ser iguales.
Producto de potencias
am·an = an+m
Es decir, se suman los exponentes.
Por ejemplo, el producto de las potencias 23 y 22 es igual a 25.
Potencia de una potencia
(am)n = an·m
Es decir, se multiplican los exponentes.
Por ejemplo, el cuadrado de 53 es igual a 56.
División de potencias
am / an = an-m
Es decir, se restan los exponentes.
Por ejemplo, la potencia 35 entre 32 es igual a 33.
Potencia negativa
a-n = 1 / (an)
Es decir, podemos eliminar el signo negativo escribiendo el inverso.
Estas propiedades son útiles tanto de izquierda a derecha como de derecha a izquierda.
Ejemplo 1
Calcular las siguientes operaciones entre potencias con bases distintas:
Solución:
Tenemos un producto de potencias en el numerador, pero no podemos calcularlo directamente porque las bases son distintas (2 y 3). En el denominador tenemos una potencia de base 6, pero podemos escribir 6 como 3·2:
Al escribir la base del denominador como un producto, tenemos las mismas bases que en el numerador y podemos aplicar las reglas.
Ejemplo 2
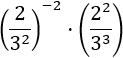
Solución:
Primero podemos eliminar el signo negativo del exponente de la primera potencia escribiendo la inversa de la fracción. Después, aplicamos las propiedades del producto, cociente y potencia de una potencia.
Recursos relacionados:
- Ejercicios de calcular y simplificar potencias (1)
- Ejercicios de calcular y simplificar potencias (2)
- Ejercicios de calcular y simplificar potencias (3)
- Problemas de operaciones con raíces (potencias con fracciones)
- Descomposición de números como producto de potencias
- Problemas de racionalizar
- Mínimo común múltiplo
- Máximo común divisor
- Problemas de mcm y MCD (1)
- Problemas de mcm y MCD (2)