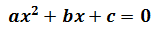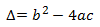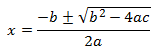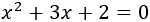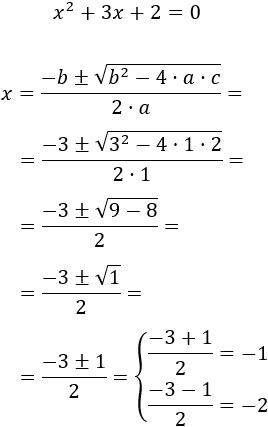Recordamos que la forma general de una ecuación cuadrática o de segundo grado es
donde a ≠ 0 , b y c los coeficientes.
Una ecuación cuadrática es completa cuando los coeficientes b y c también son distintos de 0.
Discriminante
Llamamos discriminante, Δ, de la ecuación ax 2 + bx + c = 0 a
El signo del discriminante informa acerca del número de soluciones de la ecuación:
- Si Δ es 0, la ecuación tiene una única solución (de multiplicidad 2)
- Si Δ es menor que 0, no existen soluciones (reales)
- Si Δ es mayor que 0, existen dos soluciones (reales) distintas (de multiplicidad 1).
Soluciones
Las soluciones (o raíces) de la ecuación de segundo grado (en la forma anterior) vienen dadas por la fórmula cuadrática:
Ejemplo
Vamos a resolver la siguiente ecuación
Sólo tenemos que aplicar la fórmula:
Las dos soluciones de la ecuación son x = -1 y x = -2.
Páginas con ecuaciones de segundo grado:
- Introducción a las ecuaciones de segundo grado
- Discriminante de la ecuación
- Ecuaciones incompletas resueltas
- Ecuaciones completas resueltas
- Ecuaciones con soluciones complejas
- Ecuaciones de segundo grado
- Ecuaciones incompletas resueltas (2)
- Ecuaciones completas resueltas (2)
- Propiedades de las ecuaciones cuadráticas
- Ecuaciones con soluciones complejas